Builtinmodels - stepmodel

[[Model]]
    (Model(step, prefix='step_', form='erf') + Model(linear, prefix='line_'))
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 55
    # data points      = 201
    # variables        = 5
    chi-square         = 593.709621
    reduced chi-square = 3.02913072
    Akaike info crit   = 227.700173
    Bayesian info crit = 244.216697
    R-squared          = 0.99897798
[[Variables]]
    line_slope:      1.87162383 +/- 0.09318592 (4.98%) (init = 0)
    line_intercept:  12.0964588 +/- 0.27606017 (2.28%) (init = 11.58574)
    step_amplitude:  112.858576 +/- 0.65391731 (0.58%) (init = 134.7378)
    step_center:     3.13494787 +/- 0.00516602 (0.16%) (init = 2.5)
    step_sigma:      0.67393440 +/- 0.01091158 (1.62%) (init = 1.428571)
[[Correlations]] (unreported correlations are < 0.100)
    C(line_slope, step_amplitude)     = -0.8791
    C(step_amplitude, step_sigma)     = +0.5643
    C(line_slope, step_sigma)         = -0.4569
    C(line_intercept, step_center)    = +0.4269
    C(line_slope, line_intercept)     = -0.3093
    C(line_slope, step_center)        = -0.2338
    C(line_intercept, step_sigma)     = -0.1372
    C(line_intercept, step_amplitude) = -0.1173
    C(step_amplitude, step_center)    = +0.1095

# <examples/doc_builtinmodels_stepmodel.py>
import matplotlib.pyplot as plt
import numpy as np

from lmfit.models import LinearModel, StepModel

x = np.linspace(0, 10, 201)
y = np.ones_like(x)
y[:48] = 0.0
y[48:77] = np.arange(77-48)/(77.0-48)
np.random.seed(0)
y = 110.2 * (y + 9e-3*np.random.randn(x.size)) + 12.0 + 2.22*x

step_mod = StepModel(form='erf', prefix='step_')
line_mod = LinearModel(prefix='line_')

pars = line_mod.make_params(intercept=y.min(), slope=0)
pars += step_mod.guess(y, x=x, center=2.5)

mod = step_mod + line_mod
out = mod.fit(y, pars, x=x)

print(out.fit_report())

plt.plot(x, y)
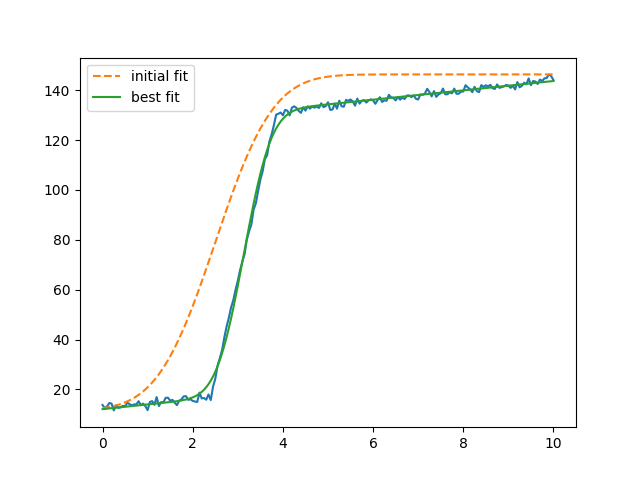
plt.plot(x, out.init_fit, '--', label='initial fit')
plt.plot(x, out.best_fit, '-', label='best fit')
plt.legend()
plt.show()
# <end examples/doc_builtinmodels_stepmodel.py>